LDA 란?
LDA (Linear Discriminant Analysis, 선형 판별 분석)
- 차원축소와 분류 에 모두 사용될 수 있는 비지도 학습 기법
- 클래스 간의 분산을 최대화하고, 클래스 내 분산을 최소화 하는 방향으로 데이터를 변환
- 데이터의 분류 성능을 향상시키고, 저차원 공간에서 데이터의 구조를 시각화할 수 있음

LDA의 주요 목표
- 차원 축소: 고차원 데이터를 저차원 공간으로 변환하여 시각화하거나, 계산 효율성을 높입니다.
- 분류 성능 향상: 차원 축소 후에, 더 구분하기 쉬운 클래스를 만드는 방향으로 데이터를 변환하여, 분류 모델의 성능을 향상시킵니다.
- 클래스 간 분리: 각 클래스가 서로 최대한 분리되도록 데이터를 변환합니다.
LDA 작동 원리
LDA는 다음과 같은 과정으로 작동합니다:
- 클래스 간 분산 (Between-class scatter):
- 각 클래스의 평균을 계산하고, 클래스의 평균 간 거리를 측정합니다.
- 클래스 간 분산을 최대화하려면 각 클래스의 평균 간 거리가 멀어야 합니다.
- 클래스 내 분산 (Within-class scatter):
- 각 클래스 내에서 데이터 포인트들이 평균으로부터 얼마나 퍼져 있는지를 측정합니다.
- 클래스 내 분산을 최소화하려면, 각 클래스 내의 데이터 포인트들이 평균에 가깝게 모여야 합니다.
- 분산 비율 최적화:
- LDA는 클래스 간 분산을 클래스 내 분산에 비해 최대화하는 투영 벡터를 찾습니다. 이 과정을 통해 클래스 분리가 가장 잘 되는 새로운 차원을 찾습니다.
- 최적화 문제 해결:
- LDA는 고유값 분해(Eigenvalue decomposition)를 사용하여, 분산 비율을 최적화하는 선형 변환을 계산합니다.
- 이 과정에서 고유값이 큰 방향(주성분)을 선택하여 데이터를 투영합니다.
수학적 공식
LDA에서 사용되는 주요 수학적 공식은 클래스 간 분산 행렬 (Between-class scatter matrix)과 클래스 내 분산 행렬 (Within-class scatter matrix)입니다.
1. 클래스 간 분산 행렬:
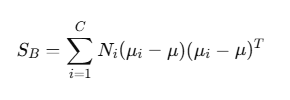

2. 클래스 내 분산 행렬:
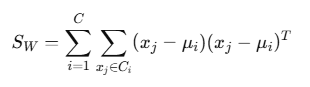

3. 최적화 목표 : LDA 는 다음의 비용함수를 최적화하는 투영 벡터를 찾습니다:
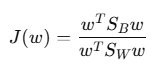
여기서 w는 투영벡터 입니다
선형 판별 축 선택
- 고유값이 큰 순서대로 고유벡터를 정렬하여 선형 판별 축을 선택
- 고유값이 클수록 해당 선형 판별 축이 클래스 간 분산을 더 많이 설명한다
- 일반적으로 클래스의 수 -1 만큼의 선형 판별 축을 선택한다
LDA의 장점
- 분류 성능 향상: LDA는 데이터의 차원을 축소하면서도 분류 성능을 향상시킬 수 있습니다.
- 구분된 클래스: 각 클래스 간의 거리가 최대화되므로, 이후 분류 작업이 더 쉬워집니다.
- 효율성: 고차원 데이터를 저차원으로 축소하여 계산 효율성을 높일 수 있습니다.
LDA의 단점
- 선형성: LDA는 선형적 특성을 가진 데이터에서 잘 작동합니다. 비선형 데이터를 처리하는 데 한계가 있을 수 있습니다.
- 정규성 가정: LDA는 각 클래스가 동일한 공분산 행렬을 가진다고 가정하는데, 이 가정이 충족되지 않으면 성능이 떨어질 수 있습니다.
- 클래스 불균형: 클래스 간 데이터 불균형이 심한 경우, LDA가 잘 작동하지 않을 수 있습니다.
예시
- 데이터 로드
from sklearn.datasets import fetch_openml
import pandas as pd
# MNIST 데이터셋 불러오기
mnist = fetch_openml('mnist_784', version=1)
# 데이터와 레이블 분리
X = mnist.data
y = mnist.target
# 데이터 프레임의 첫 5행 출력
print(X.head())
print(y.head())
- 데이터 표준화
from sklearn.preprocessing import StandardScaler
# 데이터 표준화
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
- LDA 수행
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
# LDA 모델 생성
lda = LinearDiscriminantAnalysis(n_components=9) # 클래스의 수 - 1 만큼의 선형 판별 축 선택
# LDA 학습 및 변환
X_lda = lda.fit_transform(X_scaled, y)
# 변환된 데이터의 크기 확인
print(X_lda.shape)
- LDA 결과 시각화
import matplotlib.pyplot as plt
import seaborn as sns
# 2차원 시각화
plt.figure(figsize=(10, 7))
sns.scatterplot(x=X_lda[:, 0], y=X_lda[:, 1], hue=y, palette='viridis', legend=None)
plt.title('LDA of MNIST Dataset (2D)')
plt.xlabel('LDA Component 1')
plt.ylabel('LDA Component 2')
plt.show()'AI > ML' 카테고리의 다른 글
| [ML] 앙상블 학습 - 랜덤 포레스트 (0) | 2024.12.29 |
|---|---|
| [ML] 앙상블 학습 - 배깅, 부스팅, 스태킹 (1) | 2024.12.29 |
| [ML] 비지도학습 - 차원축소 (t-SNE) (0) | 2024.12.29 |
| [ML] 비지도학습 - 차원축소 (PCA) (0) | 2024.12.29 |
| [ML] 비지도학습 - 군집화모델 (DBSCAN) (0) | 2024.12.29 |