PCA 란?
PCA (Principal Component Analysis, 주성분 분석)
- 고차원 데이터를 저차원으로 변환하는 차원 축소 기법
- PCA 는 데이터의 분산을 최대한 보존하면서, 데이터의 주요 특징을 추출해 저차원 공간으로 변환
- 데이터의 시각화, 노이즈 제거, 계산 효율성 향상 등의 이점이 있음

주요 목표
- 데이터 압축: 데이터의 구조를 최대한 유지하면서 차원을 줄여 메모리 사용량 및 계산 복잡도를 감소시킴.
- 특징 추출: 중요한 특징(주성분)을 식별해 분석 및 시각화에 활용.
- 노이즈 제거: 데이터의 주요 정보를 보존하며 불필요한 노이즈를 제거.
PCA 작동 원리
1. 평균 중심화 (Mean Centering):
- 각 데이터 특징(feature)의 평균값을 0, 분산을 1로 맞춤

2. 공분산 행렬 계산 (Covariance Matrix):
- 공분산 행렬은 데이터의 각 특성 간의 공분산을 나타내는 행렬
- 공분산 행렬을 통해 데이터의 분산과 특성 간의 상관관계를 파악 가능
- 데이터의 각 축 간 상관성을 나타내는 공분산 행렬을 계산
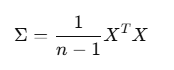
- 여기서 X 는 평균 중심화된 데이터 행렬
3. 고유값 분해 (Eigenvalue Decomposition):
- 공분산 행렬의 고유값(eigenvalue)과 고유벡터(eigenvector)를 계산합니다.
- 고유값은 주성분의 중요도를 나타내며, 고유벡터는 새로운 축(주성분)의 방향을 나타냅니다.
4. 주성분 선택:
- 고유값이 큰 순서대로 고유벡터를 정렬하여 주성분을 선택
- 고유값이 클수록 해당 주성분이 데이터의 분산을 더 많이 설명
- 일반적으로, 전체 분산의 95% 이상을 설명하는 주성분을 선택
5. 데이터 변환:
- 원래 데이터를 선택한 주성분(고유벡터) 방향으로 투영
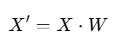
- 여기서 W 는 선택된 고유벡터로 구성된 행렬
특징
- 주성분(Principal Components): 데이터의 분산을 최대화하는 새로운 직교 축.
- 고유값(Eigenvalue): 각 주성분이 설명하는 분산의 크기.
- 차원 축소: 원래 데이터보다 적은 수의 주성분을 사용하여 데이터 표현.
장점
- 데이터 압축: 고차원 데이터를 저차원으로 변환하여 계산 효율성 향상.
- 노이즈 제거: 불필요한 변동을 제거하고 중요한 패턴을 강조.
- 시각화 가능: 2D 또는 3D로 데이터를 표현하여 이해를 돕습니다.
단점
- 해석 어려움: 주성분은 원래 변수의 선형 결합으로 생성되므로 의미 해석이 어렵습니다.
- 선형성 가정: 데이터의 선형적 관계만 고려하므로 비선형 데이터에는 한계가 있습니다.
- 스케일 민감: 데이터가 스케일링되지 않으면 결과가 왜곡될 수 있습니다.
예시
- 데이터 로드
from sklearn.datasets import fetch_openml
import pandas as pd
# MNIST 데이터셋 불러오기
mnist = fetch_openml('mnist_784', version=1)
# 데이터와 레이블 분리
X = mnist.data
y = mnist.target
# 데이터 프레임의 첫 5행 출력
print(X.head())
print(y.head())
- 데이터 표준화
from sklearn.preprocessing import StandardScaler
# 데이터 표준화
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
- PCA 수행
from sklearn.decomposition import PCA
# PCA 모델 생성
pca = PCA(n_components=0.95) # 전체 분산의 95%를 설명하는 주성분 선택
# PCA 학습 및 변환
X_pca = pca.fit_transform(X_scaled)
# 변환된 데이터의 크기 확인
print(X_pca.shape)
- 주성분 확인
# 선택된 주성분의 수
print(f'선택된 주성분의 수: {pca.n_components_}')
# 각 주성분이 설명하는 분산 비율
print(f'각 주성분이 설명하는 분산 비율: {pca.explained_variance_ratio_}')
# 누적 분산 비율
print(f'누적 분산 비율: {pca.explained_variance_ratio_.cumsum()}')
- PCA 결과 시각화
import matplotlib.pyplot as plt
import seaborn as sns
# 2차원 시각화
plt.figure(figsize=(10, 7))
sns.scatterplot(x=X_pca[:, 0], y=X_pca[:, 1], hue=y, palette='viridis', legend=None)
plt.title('PCA of MNIST Dataset (2D)')
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.show()'AI > ML' 카테고리의 다른 글
| [ML] 비지도학습 - 차원축소 (LDA) (3) | 2024.12.29 |
|---|---|
| [ML] 비지도학습 - 차원축소 (t-SNE) (0) | 2024.12.29 |
| [ML] 비지도학습 - 군집화모델 (DBSCAN) (0) | 2024.12.29 |
| [ML] 비지도학습 - 군집화모델 (계층적 군집화) (1) | 2024.12.29 |
| [ML] 비지도학습 - 군집화모델 (K-means Clustering) (2) | 2024.12.29 |